INVESTIGACION

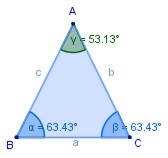
¿Cuál es el gravicentro;el ortocentro o el baricentro?

El gravímetro o centro de gravedad es el punto de intersección de las medianas del triángulo. Para ello construimos un triángulo cualquiera. Trazamos las tres medianas, es decir, las rectas que van de un vértice al punto medio del lado opuesto. El gravímetro es el punto de intersección de dos cualesquiera de las tres medianas por lo cual este punto se puede llamar GRAVICENTRO, BARICENTRO o CENTRO DE GRAVEDAD ya que es el punto donde está aplicado todo el peso de un cuerpo triangular.

BIBLIOGRAFIA:

http://arquimedes.matem.unam.mx/PUEMAC/PUEMAC_2008/geolab/practicas/gravi.html

CUADERNO DE SEGUNDO GRADO DE SECUNDARIA

biblioteca.unives.com.mx/.../15ce8b67f82714c9e3be80dae4f31753..

EJERCICIO TRES

EJERCICIO REALIZADO EL 19 DE FEBRERO DEL 2013

TEMA: TRIANGULOS.

Si el triángulo está  formado por los grados:

a) 40°,25° y 115° es un obtusángulo

b) 42°,48° y 90° es un rectángulo

c) 60°,60° y 60° es un equiángulo

d) 80°,45° y 55° es un acutángulo

EXPLICA SI EL SIGUIENTE TRIANGULO ES ISOSCELES O RECTANGULO Y ¿Por qué?

Puede ser isósceles porque tiene dos lados que son iguales pero tambien puede ser rectángulo ya que tiene un ángulo  de 90° en realidad es una mezcla de los dos.

INVESTIGACION

Mediatrices

Mediatriz es cada una de las rectas perpendiculares  que la línea empieza en la mitad de una y pasa al lado opuesto no precisamente debe ser la mitad de este lado opuesto. 

.

Bisectrices

 Corta a un ángulo exactamente a la mitad. En el caso de un triángulo la bisectriz corta a la mitad un ángulo interior.

 Habrá tres bisectrices que se intersectarán en un punto llamado INCENTRO.

Alturas

 Es el segmento que va de  un vértice hasta llegar al lado opuesto con cuidado ya  que la altura no siempre intersecta al lado del triángulo.

                           

Aquí también hay una altura para cada lado del triángulo y las alturas se intersectan en un punto llamado ORTOCENTRO. Si las alturas no se intersectan dentro del triángulo entonces hay que prolongarlas para ver el punto de intersección.

Medianas

 Segmento de recta trazado desde un vértice de un triángulo hasta el punto medio de su lado opuesto (MUY DIFERENTE AL DE LAS MEDIATRICES)

El punto donde se unen estas tres medianas es el BARICENTRO

BIBLIOGRAFIA::

http://dinamica1.fciencias.unam.mx/Preparatoria8/triangulo/mediatri.html

INVESTIGACION

CLASIFICACION DE  TRIANGULOS SUGUN SUS LADOS Y SUS ANGULOS.

Según sus lados:

Equilátero: Es el cual tiene sus tres lados iguales quiere decir que miden lo mismo y por ello sus ángulos también son iguales como se sabe la suma de los ángulos  de un triángulo es de 180º el cual en este caso cada ángulo será de 60º.

∠ ABC = ∠ BCA = ∠ CAB = 60º

Isósceles: Este tiene dos de sus lados iguales por lo tanto esos dos ángulos  también miden lo mismo.

∠ ABC = ∠ BCA

Escaleno: Sus tres lados tienen diferentes medidas así que sus tres ángulos son distintos entre sí.

Según sus ángulos:

Triángulo acutángulo: Es el que tiene sus tres ángulos agudos; es decir,  miden más de 0º y menos de 90º.

Triángulo rectángulo: Es el que tiene un ángulo recto ( 90º)

Triángulo obtusángulo: Es el que tiene un ángulo obtuso que mide más de 90º y menos de 180º.

BIBLIOGRAFIA:

http://www.aaamatematicas.com/geo318x3.htm

 

EJERCICIO DOS

EJERCICIO REALIZADO EL 12 DE FEBRERO DEL 2013

TEMA: CONSTRUCCIONES BASICAS

3.-Del segmento c localiza el punto medio y la mediatriz.

Para obtener  las dos cosas se hace lo siguiente:

1.-Con el compás centrar en A, se abre con una longitud mayor al mitad y se traza un arco de circunferencia.

2.-Con el compás centrado en B y la misma amplitud se traza un arco de circunferencia que cruce a la anterior en los puntos PQ.

3.-Trazar la recta PQ la cual será la mediatriz y el punto de intersección de ambas rectas será el punto medio(R).

 

INVESTIGACION

ANGULOS

Para empezar debemos saber que es un ángulo:

Es una figura formada por dos rectas que parten las dos de un mismo punto (el cual se conocerá como vértice).Al espacio que hay entre estas rectas se conoce como el ángulo. El símbolo del ángulo es .

Clasificación de los ángulos

Los ángulos pueden clasificarse según su medida en cinco tipos:

Ángulo recto: mide  90°

∠ α = 90°

Ángulo agudo: es menor que 90°

∠ α = < 90°

Ángulo extendido:  es de 180°

∠ α = 180°

Ángulo obtuso: es mayor que 90° y menor que 180°

∠ α = > 90° < 180º

 : 

Ángulo adyacente:
Quiere decir que dos ángulos sumados dan como resultado 180º y deben estar pegados, uno al otro deben tener un lado en común.

Ángulo opuesto al vértice.
Son  cuando los lados de uno de ellos son semirrectas de los lados del otro. Por ejemplo:

Los lados OC  y OD son las semirrectas de AO y BO

 

Ángulos complementarios y  ángulos suplementarios.

En realidad los dos son dos ángulos que juntos en el caso de los complementarios suman 90º y los suplementarios suman 180º

Obviamente deben compartir un lado de las dos rectas que la conforman.

BIBLIOGRAFIA:

http://www.profesorenlinea.cl/geometria/angulosclasificacion.htm

http://www.mathematicsdictionary.com/spanish/vmd/full/a/angle.htm

http://aulafacil.com/matematicas-basicas/geometria/curso/Lecc-12.htm

 

UNIDAD II EJERCICIO UNO

EJERCICIO REALIZADO EL 8 DE FEBRERO DEL 2013

TEMA: ELEMENTOS GEOMÉTRICOS

Contesta ¿qué elemento representa?

a) El borde de una mesa: recta

b) Una estrella en el cielo vista desde la tierra: punto

c) La página de un periódico: plano

d) El borde de una regla: recta

e) La punta de una pluma: punto

f) El filo de una espada: recta

g) La fachada de una casa: plano

EJERCICIO OCHO

EJERCICIO REALIZADO EL 1 DE FEBRERO DEL 2013

TEMA: TRASFORMACION DE UNA FUNCION ESTANDAR A GENERAL

ENCONTRAR LA FUNCION GENERAL DE LA PARABOLA QUE TIENE EL VERTICE (1,3) Y UNA A=4

4(x-1)²+3=f(x)

4(x²-2x+1)+3=f(x)

4x²-8x+4+3=f(x)

4x²-8x+7=f(x)

EJERCICIO SIETE

EJERCICIO REALIZADO EL DIA 31 DE ENERO DEL 2013

TEMA: DE FORMA GENERAL A FORMA ESTANDAR.

(Cuando el coeficiente cuadrático es diferente a 1)

Transforma la siguiente función a forma estándar y graficar.

1.-2x²-12x+19

Primero agrupamos los términos cuadráticos.

[2x²-12x ]+19

Se factoriza lo que agrupamos.

2 [ x²-6x]+19

Se obtiene b del termino lineal.

(-6÷2)²=9

Se suma y se resta el valor obtenido en los corchetes

2 [x²-6x+9-9 ]+19

Se factoriza para obtener el trinomio cuadrado perfecto.

2 [(x-3)² -9]+19

Jerarquía de operaciones

2(x-3)²-18+19

2(x-3)²+1

A=2

H=3

K=1

Vértice :(3,-1)

Se tabula

x	y
5	9
4	3
3	1
2	3
1	9

Se grafica

ELEMENTOS

Ramas: arriba

 Concavidad: positiva

Vértice: (3,1)

Eje de simetría: 3

Mínimo: 1

 

 

 

 

 

 

 

EJERCICIO SEIS

EJERCICIO REALIZADO EL DIA  29 DE ENERO DEL 2013

TEMA: CONVERSION DE FORMA GENERAL  A FORMA ESTANDAR
(cuando el valor de a es igual a 1)

De la siguiente función obtener sus elementos y grafica transformándolo a forma estándar.

Y=x²+6x+7

A=1

B=6

C=7

(b÷2)²    (6÷2)²=9

Y=x²+6x+9-9+7

Y=x²+6x+9-9+7

x² se toma su raíz

+6x se toma su signo

9 se toma su raíz

Y=(x+3)²-9+7

Y=(x+3)²-2

A=1

H=-3

K=-2

Vértice:(-3,-2)

Se tabula

x	y
-5	2
-4	-1
-3	-2
-2	-1
-1	2

 

Operaciones

Y=(-5)²+6(-5)+7

Y=2

Y=(-4) ²+6(-4)+7

Y=-1

Y=(-2)²+6(-2)+7

Y=-1

Y=(-1)²+6(-1)+7

Y=2

Se grafica

 

Elementos:

Ramas: arriba

Concavidad: positiva

Vértice:(-3,-2)

Eje de simetría:-3

Mínimo:-2